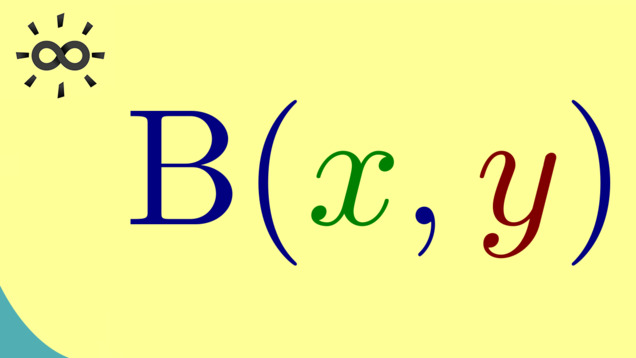
-
Title: Beta Function
-
Series: Advent of Mathematical Symbols
-
YouTube-Title: Advent of Mathematical Symbols - Part 15 - Beta Function
-
Bright video: https://youtu.be/q3IPaNVoA18
-
Dark video: https://youtu.be/6K88pAs2er8
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: aoms15_sub_eng.srt
-
Timestamps (n/a)
-
Subtitle in English
1 00:00:00,671 –> 00:00:04,309 The mathematical symbol of today is the so called beta function.
2 00:00:04,509 –> 00:00:07,013 Which is denoted with the greek letter beta.
3 00:00:07,771 –> 00:00:11,933 However you see it’s the capital letter, which looks like a normal B.
4 00:00:13,000 –> 00:00:16,629 Now the beta function has two variables as its input.
5 00:00:16,686 –> 00:00:18,875 So lets call them x and y.
6 00:00:20,000 –> 00:00:23,503 Indeed x and y could be complex numbers.
7 00:00:24,557 –> 00:00:28,749 However then the real part of both numbers should be positive.
8 00:00:29,757 –> 00:00:35,182 So we write: real part of x greater than 0 and real part of y greater than 0.
9 00:00:36,286 –> 00:00:40,957 Ok by knowing this we now can write down the definition of the beta function.
10 00:00:42,100 –> 00:00:46,442 and indeed it’s given by an integral from 0 to 1.
11 00:00:47,314 –> 00:00:50,514 and the variable we integrate over we call t.
12 00:00:51,314 –> 00:00:55,271 Now the first t here has a power, where x occurs.
13 00:00:56,171 –> 00:00:59,190 Indeed the exponent is (x - 1).
14 00:01:00,071 –> 00:01:04,886 and then comes the factor (1 - t), where in the power we find y.
15 00:01:05,729 –> 00:01:08,711 More precisely it’s (y - 1).
16 00:01:09,700 –> 00:01:13,038 Ok so this is the whole definition of the beta function.
17 00:01:13,986 –> 00:01:18,921 and when you already know the gamma function i can tell you an important identity.
18 00:01:19,729 –> 00:01:24,552 Indeed the beta function and the gamma function are closely connected.
19 00:01:25,343 –> 00:01:38,799 More concretely B(x, y) can be written as “gamma(x) times gamma(y) divided by gamma(x + y).”
20 00:01:39,943 –> 00:01:46,902 This can be proven when you use the integral definition of the beta function and the integral definition of the gamma function.
21 00:01:48,014 –> 00:01:56,518 and now i can also tell you, because the gamma function is related to the factorial, the beta function is related to the binomial coefficient.
22 00:01:57,529 –> 00:02:00,295 However that can be a whole topic for another video.
23 00:02:01,257 –> 00:02:05,875 Here you have seen the definition of the beta function and i hope that this was helpful.
24 00:02:06,671 –> 00:02:08,799 In this case i see you next time.
25 00:02:08,999 –> 00:02:09,629 Bye!
-
Quiz Content
Q1: What is the correct definition of the Beta function?
A1: $B(x,y) = \int_0^1 t^{x-1} (1-t)^{y-1}, dt$
A2: $B(x,y) = \int_0^1 t^{x-1} t^{y-1}, dt$
A3: $B(x,y) = \int_0^1 x^{t-1} (1-t)^{y-1}, dt$
A4: $B(x,y) = \int_0^1 x^{t-1} (1-x)^{t-1}, dt$
A5: $B(x,y) = \int_0^1 x^{t-1} (1-x)^{x-1}, dx$
Q2: What is the correct property for the Beta function?
A1: $B(x,y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)}$
A2: $B(x,y) = \Gamma(x) \Gamma(y) \Gamma(x+y)$
A3: $B(x,y) = \Gamma(x) \Gamma(x+y)$
A4: $B(x,y) = \Gamma(x) \Gamma(y) $