-
Title: Examples for Limit Superior and Limit Inferior
-
Series: Real Analysis
-
Chapter: Sequences and Limits
-
YouTube-Title: Real Analysis 12 | Examples for Limit Superior and Limit Inferior
-
Bright video: https://youtu.be/afDgCWY8DOY
-
Dark video: https://youtu.be/HozOmFX2Ef0
-
Ad-free video: Watch Vimeo video
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Exercise Download PDF sheets
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: ra12_sub_eng.srt
-
Timestamps
00:00 Intro
00:37 Example
01:31 Properties of lim sup and lim inf
03:00 Properties for combining 2 sequences
04:53 Example summation of 2 sequences
06:00 Example product of 2 sequences
06:57 Credits
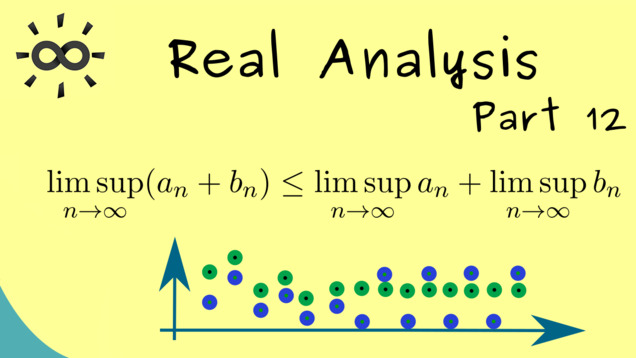
-
Subtitle in English
1 00:00:00,414 –> 00:00:03,191 Hello and welcome back to real analysis
2 00:00:03,929 –> 00:00:08,892 and of course many, many thanks to all the nice people that support this channel on Steady or Paypal.
3 00:00:09,092 –> 00:00:13,626 In today’s part 12 we talk again about the limit superior and the limit inferior.
4 00:00:14,386 –> 00:00:20,489 Here please recall, for any sequence of real numbers this lim sup and lim inf always exist.
5 00:00:20,771 –> 00:00:25,841 Namely they are either a real number or the symbol - or + infinity.
6 00:00:26,041 –> 00:00:30,117 Also I can tell you, some people write this set as an interval.
7 00:00:30,657 –> 00:00:36,738 There we use brackets to say that the symbols -infinity and infinity are included in the set.
8 00:00:36,938 –> 00:00:40,899 Ok, since you already know this, let’s look at an example.
9 00:00:41,343 –> 00:00:47,739 So here i take the sequence a_n given as (-1) to the power n times n.
10 00:00:47,939 –> 00:00:56,516 Hence the sequence starts with -1, then comes 2, then -3, then 4, -5 and so on.
11 00:00:57,014 –> 00:01:00,442 Obviously this sequence is not convergent.
12 00:01:00,642 –> 00:01:04,978 However we find a subsequence that is divergent to infinity.
13 00:01:05,178 –> 00:01:08,323 Hence the lim sup has to be infinity.
14 00:01:08,757 –> 00:01:13,693 Then in the same way we find a subsequence that is divergent to -infinity.
15 00:01:14,286 –> 00:01:17,419 Hence the lim inf has to be -infinity.
16 00:01:17,957 –> 00:01:20,043 So you see this is a simple example,
17 00:01:20,086 –> 00:01:27,271 but it tells us that all the elements in this set are possible values for the limit superior and limit inferior.
18 00:01:27,871 –> 00:01:30,884 With this in mind let’s formulate some properties.
19 00:01:31,343 –> 00:01:34,806 First let’s discuss what we have for convergent sequences.
20 00:01:35,257 –> 00:01:41,410 Here please recall, the lim sup is the largest accumulation value and the lim inf the smallest one.
21 00:01:41,610 –> 00:01:48,036 Therefore a sequence is convergent if and only if the lim sup and the lim inf are actually the same
22 00:01:48,236 –> 00:01:50,968 and of course they should be real numbers.
23 00:01:51,429 –> 00:01:57,106 This is not hard to see, if the sequence is convergent lim sup and lim inf are actually the limit.
24 00:01:57,306 –> 00:02:05,214 On the other hand if they are the same, there is only one accumulation value, therefore the sequence has to converge to this value.
25 00:02:05,414 –> 00:02:10,970 Ok, now we can extend this result and talk about the case when the limit is infinity.
26 00:02:11,170 –> 00:02:14,419 So we say the sequence is divergent to infinity.
27 00:02:14,900 –> 00:02:19,799 Then lim sup and lim inf have to be the same again, but now they should be infinity.
28 00:02:20,686 –> 00:02:27,593 Please compare this to the example, because there it’s different. They are not real numbers, but they are not the same.
29 00:02:27,793 –> 00:02:35,053 Ok, another thing i can tell you is that the lim sup is always the largest accumulation value. So always larger than lim inf.
30 00:02:35,253 –> 00:02:37,643 Therefore we can just ignore this part here.
31 00:02:37,800 –> 00:02:41,966 This immediately follows if you know that the lim inf is infinity.
32 00:02:42,514 –> 00:02:48,044 Now next, maybe not so surprising, we can do the same for the limit -infinity
33 00:02:48,244 –> 00:02:53,068 and this holds if and only if the lim sup is -infinity.
34 00:02:53,814 –> 00:02:59,916 Now, all the things here are easy to show, when you know the definitions we discussed in the last video.
35 00:03:00,429 –> 00:03:05,629 A little bit more complicated is the next property, where we combine 2 different sequences.
36 00:03:06,371 –> 00:03:12,286 Ok, now for a sequence a_n and b_n you could ask: “What is the lim sup of the sum?”
37 00:03:12,686 –> 00:03:15,252 So lim sup (a_n + b_n).
38 00:03:15,452 –> 00:03:20,020 In general this is not equal to the sum of the two limit superiors,
39 00:03:20,729 –> 00:03:22,989 but only less or equal.
40 00:03:23,686 –> 00:03:29,912 However please keep in mind, this only makes sense if the right-hand side here, is well defined.
41 00:03:30,286 –> 00:03:35,638 For example infinity + (-infinity) would be not defined.
42 00:03:36,029 –> 00:03:43,995 Now, this is the only exception of this inequality. For example you could have infinity + 5 and this would be infinity again.
43 00:03:44,400 –> 00:03:49,882 Ok, now in the same way, for 2 sequences you could ask: “What is about the product?”
44 00:03:50,082 –> 00:03:58,833 and it turns out, it’s the same thing. The lim sup of (a_n times b_n) is less or equal than the product of the 2 limit superiors.
45 00:03:59,214 –> 00:04:06,816 However, in general this is not correct, because we could have different signs for the sequences, which would flip the inequality.
46 00:04:07,314 –> 00:04:12,361 Therefore let’s formulate and remember this property for non-negative sequences.
47 00:04:12,857 –> 00:04:19,574 However also here we have an exception, for example 0 times infinity is not defined.
48 00:04:19,774 –> 00:04:25,178 This is important to know, whenever you calculate with the symbols - and + infinity.
49 00:04:25,771 –> 00:04:30,751 Ok, i would say proving these two inequalities is a very good exercise for you,
50 00:04:31,200 –> 00:04:37,392 because when you do this, you immediately see that we have a similar inequality for the limit inferior.
51 00:04:37,829 –> 00:04:42,972 So it’s the same in green here. The only thing that changed is the direction of the inequality.
52 00:04:43,172 –> 00:04:47,420 So the lim inf on the left-hand side could get bigger than the right-hand side.
53 00:04:48,200 –> 00:04:53,315 To see that this is in general really an inequality let’s look at an example.
54 00:04:53,971 –> 00:04:57,076 So here we need two sequences of real numbers.
55 00:04:57,657 –> 00:05:03,093 I want a_n to be 1, -1, 1, -1 and so on
56 00:05:03,293 –> 00:05:07,907 and b_n to be 0, 2, 0, 2 and so on.
57 00:05:08,329 –> 00:05:12,736 With this information we can immediately calculate the sum of the two sequences.
58 00:05:13,371 –> 00:05:17,514 Which is simply the constant sequence with value 1.
59 00:05:17,600 –> 00:05:19,943 Hence simply a convergent sequence.
60 00:05:20,857 –> 00:05:25,483 Therefore the lim sup and the lim inf of the sum are simply 1
61 00:05:25,683 –> 00:05:30,010 and now we know from the properties above that we have inequalities here.
62 00:05:30,386 –> 00:05:33,852 Indeed, here in this case they are actually strict,
63 00:05:34,052 –> 00:05:39,035 because here on the right-hand side we have 1 + 2, which is 3.
64 00:05:39,235 –> 00:05:41,801 Which is strictly greater than 1
65 00:05:42,271 –> 00:05:49,817 and for the lim inf, we have -1 + 0. So also here strictly less than 1.
66 00:05:50,386 –> 00:05:54,077 Ok, now of course we can do the same for the product.
67 00:05:54,277 –> 00:05:57,476 However, for this we should take non-negative sequences.
68 00:05:57,943 –> 00:06:01,415 Therefore let’s formulate this with a new example.
69 00:06:01,943 –> 00:06:08,627 So we can take the same sequence for b_n, but for a_n we have to substitute -1 with 0.
70 00:06:09,014 –> 00:06:14,266 Then the product sequence is just the constant sequence, now with 0 as the value.
71 00:06:14,729 –> 00:06:18,221 Of course then the lim sup is 0 as well.
72 00:06:18,421 –> 00:06:24,465 On the other hand the lim sup of a_n is 1 and the lim sup of b_n is 2.
73 00:06:24,665 –> 00:06:27,071 So we have 2 on the right-hand side.
74 00:06:27,686 –> 00:06:32,576 Therefore also here, we see in this example we have the strict inequality.
75 00:06:33,314 –> 00:06:40,956 Ok, after all this the important things you really should remember are the 4 inequalities we have for lim sup and lim inf
76 00:06:41,414 –> 00:06:47,069 and when you have time, maybe you also find an example, where we have the strict inequality for lim inf.
77 00:06:47,571 –> 00:06:52,604 Later you will see, we can use these inequalities a lot in calculations.
78 00:06:53,157 –> 00:06:56,733 Ok, I think that’s good enough for today and I hope I see you next time.
79 00:06:56,814 –> 00:06:57,543 Bye!
-
Quiz Content
Q1: Which one of the following statements is not true in general?
A1: $ \displaystyle \liminf_{n \rightarrow \infty} a_n \leq \limsup_{n \rightarrow \infty} a_n$
A2: $ \displaystyle \liminf_{n \rightarrow \infty} a_n = \limsup_{n \rightarrow \infty} a_n$ $
\Rightarrow$ $(a_n)$ is convergentA3: $(a_n)$ is convergent $
\Rightarrow$ $ \displaystyle \liminf_{n \rightarrow \infty} a_n = \limsup_{n \rightarrow \infty} a_n$A4: $\displaystyle \liminf_{n \rightarrow \infty} a_n = \infty$ $
\Rightarrow$ $ \displaystyle \limsup_{n \rightarrow \infty} a_n = \infty $Q2: Consider the sequence $(a_n)_{n\in \mathbb{N}}$ given by $$a_n = (1,2,1,3,1,4,1,5,1,6,1,7,\ldots)$$ What is the limit inferior and limit superior of this sequence?
A1: $\displaystyle \liminf_{n \rightarrow \infty} a_n = \infty$ and $\displaystyle \limsup_{n \rightarrow \infty} a_n = \infty$
A2: $\displaystyle \liminf_{n \rightarrow \infty} a_n = 0$ and $\displaystyle \limsup_{n \rightarrow \infty} a_n = \infty$
A3: $\displaystyle \liminf_{n \rightarrow \infty} a_n = -\infty$ and $\displaystyle \limsup_{n \rightarrow \infty} a_n = \infty$
A4: $\displaystyle \liminf_{n \rightarrow \infty} a_n = 1$ and $\displaystyle \limsup_{n \rightarrow \infty} a_n = \infty$
A5: $\displaystyle \liminf_{n \rightarrow \infty} a_n = 1$ and $\displaystyle \limsup_{n \rightarrow \infty} a_n = 1$
Q3: For which one of the following statements there is no example of two sequences $(a_n){n\in \mathbb{N}}$ and $(b_n){n\in \mathbb{N}}$, where $a_n, b_n \geq 0$, such that the statement is true?
A1: $$ \limsup_{n \rightarrow \infty} (a_n + b_n) < \limsup_{n \rightarrow \infty} a_n + \limsup_{n \rightarrow \infty} b_n$$
A2: $$ \liminf_{n \rightarrow \infty} (a_n \cdot b_n) < \liminf_{n \rightarrow \infty} a_n \cdot \liminf_{n \rightarrow \infty} b_n$$
A3: $$ \limsup_{n \rightarrow \infty} (a_n \cdot b_n) < \limsup_{n \rightarrow \infty} a_n \cdot \limsup_{n \rightarrow \infty} b_n$$
A4: $$ \liminf_{n \rightarrow \infty} (a_n + b_n) > \liminf_{n \rightarrow \infty} a_n + \liminf_{n \rightarrow \infty} b_n$$
-
Last update: 2025-01