-
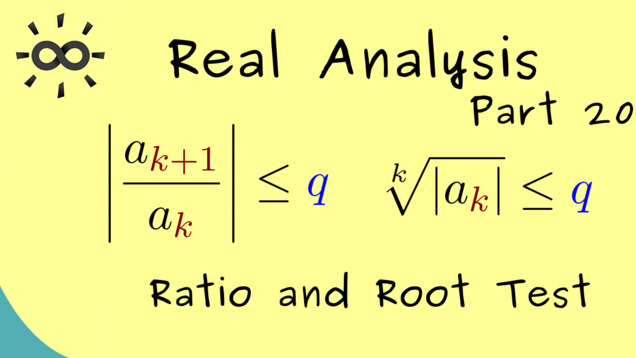
Title: Ratio and Root Test
-
Series: Real Analysis
-
Chapter: Infinite Series
-
YouTube-Title: Real Analysis 20 | Ratio and Root Test
-
Bright video: https://youtu.be/yLbgdL9HAeg
-
Dark video: https://youtu.be/a9aoJB6VDOc
-
Ad-free video: Watch Vimeo video
-
Quiz: Test your knowledge
-
Dark-PDF: Download PDF version of the dark video
-
Print-PDF: Download printable PDF version
-
Exercise Download PDF sheets
-
Thumbnail (bright): Download PNG
-
Thumbnail (dark): Download PNG
-
Subtitle on GitHub: ra20_sub_eng.srt
-
Timestamps
00:00 Intro
00:50 Recalling the geometric series
01:26 Proposition
02:33 Ratio test
03:43 Proof of the ratio test
05:14 Example using the ratio test
07:01 Root test
07:37 Proof of the root test
08:21 Example using the root test
09:15 Root criterion (limit form)
10:58 Credits
-
Subtitle in English
1 00:00:00,471 –> 00:00:03,655 Hello and welcome back to real analysis
2 00:00:03,855 –> 00:00:09,381 and as always many, many thanks to all the nice people that support this channel on Steady or PayPal.
3 00:00:10,071 –> 00:00:17,494 In today’s part 20 we will talk about two important criteria we have for the convergence or the divergence of a series.
4 00:00:18,143 –> 00:00:21,921 They are simply called the ratio test and the root test
5 00:00:22,214 –> 00:00:28,290 In the best case scenario they answer the question if a given series is absolutely convergent.
6 00:00:28,586 –> 00:00:31,676 Here please recall we have already learned in the last video,
7 00:00:31,876 –> 00:00:36,486 if we have a convergent majorant, this series is absolutely convergent.
8 00:00:36,791 –> 00:00:39,391 This is known as the comparison test.
9 00:00:39,914 –> 00:00:43,987 The only problem here is that we really have to find such a majorant.
10 00:00:44,443 –> 00:00:49,376 Therefore we might try to use some series, where we already know that they are convergent.
11 00:00:49,771 –> 00:00:53,744 For example we already know the famous geometric series.
12 00:00:53,944 –> 00:00:58,857 As a reminder let’s state the fact again, which holds for the geometric series.
13 00:00:59,057 –> 00:01:08,566 We know that summing up the powers of q gives us a convergence series, if and only if this q is in the absolute value less than 1.
14 00:01:08,766 –> 00:01:15,166 We need this fact for real numbers q, but I can tell you it also holds for complex numbers q.
15 00:01:15,729 –> 00:01:20,109 This is good to know in the case that you also watch my complex analysis course.
16 00:01:20,309 –> 00:01:25,750 Ok, now here we will apply the comparison test by using the geometric series
17 00:01:26,214 –> 00:01:29,231 and let’s put all of this in a proposition.
18 00:01:29,586 –> 00:01:36,000 So if we find an index n_0 and a number q, which is in the absolute value less than 1
19 00:01:36,429 –> 00:01:45,814 and with the property that the absolute value of a_k is less than q to the power k, for all k greater or equal than n_0,
20 00:01:46,114 –> 00:01:50,051 then this series a_k is absolutely convergent.
21 00:01:50,251 –> 00:01:53,954 This is simply the majorant criterion from the last video
22 00:01:54,229 –> 00:01:58,755 and we just use the convergent geometric series for the majorant.
23 00:01:59,214 –> 00:02:06,239 Ok, we can change it a little bit, because we don’t destroy the convergence when we multiply the series with a constant.
24 00:02:06,439 –> 00:02:12,273 Therefore we can simply introduce a constant capital C here and we have the same result.
25 00:02:12,473 –> 00:02:18,717 Now again this is simply the majorant criterion which might be helpful if you want to check for convergence.
26 00:02:19,157 –> 00:02:24,456 Still here you have to find a suitable q such that this inequality is fulfilled.
27 00:02:24,656 –> 00:02:29,226 Therefore it might be psychologically helpful to rewrite the whole thing
28 00:02:29,426 –> 00:02:33,662 and one possibility leads us to something we call the ratio test.
29 00:02:34,171 –> 00:02:42,551 There we just have to calculate a quotient. Namely we just take a_(k+1) and divide it by a_k
30 00:02:42,751 –> 00:02:52,097 and if this is measured with the absolute value, less or equal than q for all k, then the series is absolutely convergent.
31 00:02:52,543 –> 00:03:00,750 For some examples this can be very helpful when you can calculate this fraction or when you can estimate it very easily.
32 00:03:01,143 –> 00:03:07,151 Of course for the correct formulation here, we have to choose our n_0 again and the number q.
33 00:03:07,351 –> 00:03:12,814 In order to make this formulation simpler we can just choose q between 0 and 1,
34 00:03:13,014 –> 00:03:16,372 because obviously a negative q won’t work here.
35 00:03:16,943 –> 00:03:19,998 However please keep in mind, 1 is excluded here.
36 00:03:20,686 –> 00:03:26,594 Ok, so we want this inequality here eventually, so for all k greater or equal than n_0.
37 00:03:27,186 –> 00:03:33,059 However we can only have that if the denominator here is always non-zero.
38 00:03:33,571 –> 00:03:37,298 Hence to be correct we have to include this information here as well.
39 00:03:37,857 –> 00:03:43,649 Now before we do an example let me show you the proof of the ratio test, which is very short.
40 00:03:43,849 –> 00:03:46,771 Indeed we have already all the information we need.
41 00:03:47,329 –> 00:03:52,133 In the first step let’s multiply this inequality with the denominator.
42 00:03:52,657 –> 00:03:58,302 Then we get this nice inequality which holds for all k greater or equal than n_0.
43 00:03:58,900 –> 00:04:04,002 This means we can apply it again on the right-hand side, where we have the absolute value of a_k.
44 00:04:04,557 –> 00:04:08,642 In other words we have here q times a_(k-1)
45 00:04:08,842 –> 00:04:14,251 and then we can do this again and again until this index here is n_0
46 00:04:14,814 –> 00:04:20,158 I just say you can do this inductively, because the formal proof would be a proof by induction.
47 00:04:20,571 –> 00:04:26,193 Ok and here we just have to count how many steps we have. So how many factors q we have
48 00:04:26,393 –> 00:04:29,800 and it turns out we have k+1-n_0.
49 00:04:30,286 –> 00:04:35,664 Of course we can just rewrite this if you want with the correct factor k+1.
50 00:04:35,864 –> 00:04:39,247 Simply by dividing with q to the power n_0.
51 00:04:39,629 –> 00:04:43,923 There you see both things together gives us this power back.
52 00:04:44,123 –> 00:04:51,352 We do this because now this whole inequality, left-hand side and right-hand side is of this form here.
53 00:04:51,600 –> 00:04:55,243 Where our constant c is simply this fraction here.
54 00:04:55,971 –> 00:05:02,796 However this whole thing now means that all the requirements of the majorant criterion are satisfied.
55 00:05:03,357 –> 00:05:09,433 Hence we can conclude that the series is absolutely convergent and we have proven the ratio test.
56 00:05:10,129 –> 00:05:14,793 Ok, so now let’s demonstrate how helpful this test can be with an example.
57 00:05:14,993 –> 00:05:19,688 Here let’s consider the series with 1 over k factorial.
58 00:05:20,214 –> 00:05:24,078 The question for you is now: “Is this a convergent series?”.
59 00:05:24,743 –> 00:05:30,162 Now, because there is a fraction involved, maybe the ratio test gives immediately an answer.
60 00:05:30,657 –> 00:05:34,039 Therefore I would say just let’s calculate this fraction here.
61 00:05:34,700 –> 00:05:38,876 We just have positive numbers. Therefore we can omit the absolute values.
62 00:05:39,400 –> 00:05:45,395 Ok, so this is the fraction and now we can use, that we know what (k+1) factorial is.
63 00:05:45,595 –> 00:05:49,592 It is simply k factorial multiplied with (k+1).
64 00:05:49,829 –> 00:05:54,869 This means that everything cancels out here, except one factor, k+1
65 00:05:55,069 –> 00:05:58,667 and the crucial thing here is, it’s in the denominator.
66 00:05:59,243 –> 00:06:03,975 Therefore we immediately see, this is always less or equal than 1/2.
67 00:06:04,629 –> 00:06:09,736 Hence this 1/2 is our q and n_0 we can choose as 1.
68 00:06:09,936 –> 00:06:15,450 Of course if you would choose a larger n_0, you could choose a smaller q.
69 00:06:15,650 –> 00:06:21,193 However this is not important. The important thing is that you can choose q less than 1
70 00:06:21,393 –> 00:06:23,944 and of course 1/2 is a good choice here.
71 00:06:24,514 –> 00:06:29,293 Ok and there you see, we are already finished. This series is convergent.
72 00:06:29,493 –> 00:06:35,634 Now, before we go to the next test, I should warn you that you really should be careful in your calculations.
73 00:06:36,286 –> 00:06:41,930 If you just show that this fraction is strictly less than 1, this is not enough!
74 00:06:42,130 –> 00:06:48,301 Of course it looks similar to the inequality we want, but please note it’s not the same
75 00:06:48,501 –> 00:06:51,628 and also, you already know a good example for this.
76 00:06:52,000 –> 00:06:55,314 Namely the harmonic series. Which is divergent.
77 00:06:55,929 –> 00:07:01,337 Ok with this in mind let’s go to another important test, the root test.
78 00:07:01,729 –> 00:07:06,788 As the name suggests, here we don’t look at a ratio as before, but at a root.
79 00:07:07,314 –> 00:07:12,249 More concretely we will look at the kth root of a_k in the absolute value
80 00:07:13,014 –> 00:07:17,264 and as before this should be less or equal than a given q
81 00:07:17,464 –> 00:07:21,868 and the overall assumptions for q are of course the same as before
82 00:07:22,386 –> 00:07:26,580 and then we can conclude that the series is absolutely convergent.
83 00:07:27,229 –> 00:07:32,754 Here you see unlike the ratio test, the root test does not need that a_k is non-zero.
84 00:07:33,243 –> 00:07:36,255 In this sense we have fewer assumptions here.
85 00:07:36,455 –> 00:07:42,717 Ok, then let’s write down the proof, but I can tell you, it’s probably the simplest proof we have ever done in this course,
86 00:07:43,329 –> 00:07:48,367 because in this inequality we can simply use the kth power on both sides
87 00:07:49,086 –> 00:07:54,575 and then we simply have that q to the power k is a majorant for a_k
88 00:07:54,775 –> 00:08:00,342 or in other words, we have the geometric series as a convergent series in our comparison test
89 00:08:01,014 –> 00:08:05,544 and this immediately gives us that the series is absolutely convergent.
90 00:08:05,843 –> 00:08:12,480 Therefore one could say the root test is exactly the same as the comparison test with the geometric series.
91 00:08:12,943 –> 00:08:18,494 Still, this formulation might be easier for you, because you have something you can calculate.
92 00:08:18,814 –> 00:08:21,739 Let’s simply demonstrate that with an example.
93 00:08:22,143 –> 00:08:27,120 So here we have a maybe complicated looking series, but there is a power involved.
94 00:08:27,686 –> 00:08:32,929 Hence the root test could be suitable to answer the question: if this series is convergent.
95 00:08:33,371 –> 00:08:36,709 So for the coefficient we take the kth root.
96 00:08:36,909 –> 00:08:40,908 Then the power cancels out and only the power 2 remains.
97 00:08:41,386 –> 00:08:47,860 Hence we only have the fraction 9 over (2+k), which is less or equal than 9 over 10.
98 00:08:48,114 –> 00:08:51,918 Of course this only holds for k that are greater or equal than 8.
99 00:08:52,557 –> 00:08:57,988 In summary there we have our n_0 and there we have our q that is less than 1.
100 00:08:58,188 –> 00:09:03,790 Therefore we can conclude, this series is indeed convergent. Namely by our root test.
101 00:09:04,229 –> 00:09:08,981 Ok, so this was an example how you can apply this nice criterion.
102 00:09:09,181 –> 00:09:15,732 However we can make it even better by avoiding that we have to choose q and n_0 in the end.
103 00:09:15,932 –> 00:09:21,962 Indeed this works, because we can reformulate the whole statement with the limit superior.
104 00:09:22,162 –> 00:09:28,700 In fact this is what you should remember. You can calculate the limit superior of the kth root of a_k
105 00:09:29,343 –> 00:09:34,765 and if the result is strictly less than 1, our root test is fulfilled.
106 00:09:34,965 –> 00:09:41,816 In other words all the requirements are fulfilled and we can conclude that the series is absolutely convergent.
107 00:09:42,571 –> 00:09:47,769 In our example from before we just have to look at the limit superior of this result here.
108 00:09:47,969 –> 00:09:50,747 Which is in this case simply 0.
109 00:09:50,947 –> 00:09:57,666 Hence I think this is very helpful, psychologically helpful, because you don’t have to guess a suitable q.
110 00:09:57,866 –> 00:10:01,554 You simply get a number out and you can check if this is less than 1.
111 00:10:02,186 –> 00:10:05,856 Also what one can prove is that it works the other way around.
112 00:10:06,414 –> 00:10:13,997 Meaning if the lim sup we calculate is strictly greater than 1, then the corresponding series is divergent.
113 00:10:14,386 –> 00:10:20,653 This also follows from the comparison test with the geometric series, but now with the minorant criterion.
114 00:10:21,143 –> 00:10:24,786 Ok, so please remember the whole thing here for the root test
115 00:10:24,986 –> 00:10:33,555 and please also remember if it happens that you get out 1 for the lim sup, we are not able to say what happens for the series.
116 00:10:34,114 –> 00:10:36,762 Indeed 3 cases are possible then.
117 00:10:37,171 –> 00:10:40,267 The first case would be: the series is divergent
118 00:10:40,467 –> 00:10:43,515 and the second case would be: it is absolutely convergent
119 00:10:43,715 –> 00:10:48,559 and the third case would be: it’s neither of them. It’s just convergent.
120 00:10:48,759 –> 00:10:51,273 Ok, I thing that’s good enough for today.
121 00:10:51,473 –> 00:10:57,757 In the next video we will still talk about series and I hope I see you there. Have a nice day. Bye!
-
Quiz Content
Q1: For which $q \in \mathbb{R}$ is the series $\displaystyle \sum_{k = 0}^\infty q^k$ convergent?
A1: Only for $q = 0$
A2: For none.
A3: Only for $|q| < 1$.
A4: Only for $|q| \leq 1$.
A5: Only for $|q| \geq 1$.
Q2: What is the correct formulation for the ratio test?
A1: If there is $n_0$ and $q \in [0,1]$ with $\left| \frac{a_{k+1}}{a_k} \right| < q$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
A2: If there is $n_0$ and $q \in [0,1)$ with $a_k \neq 0$ and $\left| \frac{a_{k+1}}{a_k} \right| < q$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
A3: If there is $n_0$ with $a_k \neq 0$ and $\left| \frac{a_{k+1}}{a_k} \right| < 1$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
A4: If there is $n_0$ and $q \in [0,1)$ with $a_k \neq 0$ and $\left| \frac{a_{k}}{a_{k+1}} \right| < 1$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
Q3: What is the correct formulation for the root test?
A1: If there is $n_0$ and $q \in [0,1]$ with $\left| \sqrt[k]{a_k} \right| < q$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
A2: If there is $n_0$ and $q \in [0,1)$ with $\left| \sqrt[k]{a_k} \right| > q$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
A3: If there is $n_0$ and $q \in [0,1]$ with $\left| \sqrt[k]{a_k} \right| > q$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
A4: If there is $n_0$ and $q \in [0,1)$ with $\left| \sqrt[k]{a_k} \right| < q$ for all $k \geq n_0$, then the series $\displaystyle \sum_{k = 1}^\infty a_k$ is absolutely convergent.
Q4: Is the series $\displaystyle \sum_{k = 0}^\infty \frac{2^k}{k!}$ convergent?
A1: Yes, you can apply the ratio test.
A2: No, the root test shows divergence.
-
Last update: 2025-01